내용:
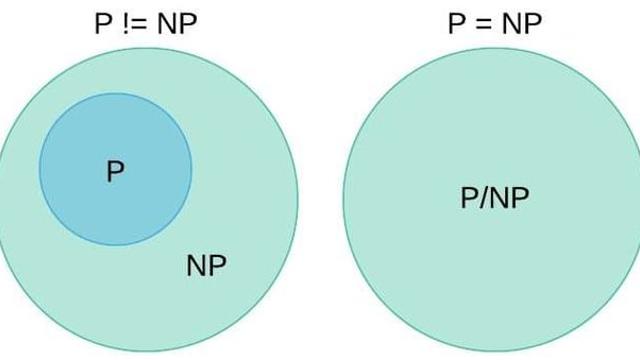
P vs NP 문제(이론 컴퓨터 과학)
모든 NP는 P인가?
-> “모든 쉽게 검산 가능한 문제는 쉽게 풀 수 있는 문제에 속하는가?” 를 질문하는 문제
리만 가설(정수론)
리만 제타 함수 ζ(s)=0을 만족시키는 모든 자명하지 않은 근의 실수부는 1/2이다.
-> 소수의 규칙성에 관한 문제
나비에-스토크스 방정식의 해의 존재와 매끄러움(유체역학)
모든 초기 조건에 대해 3차원 유체 흐름 방정식(나비에-스토크스 방정식)의 해가 존재하거나 매끄러운가?
-> 유체의 흐름에 관한 문제
버치-스위턴다이너 추측(정수론)
수체 상의 타원곡선 E의 점들이 이루는 아벨 군의 계수와 그 하세-베유 L-함수 L(E, s)의 s = 1에서 갖는 근의 차수가 같은가?
-> 타원 곡선 위의 정수해들의 규칙에 관한 문제
호지 추측(대수기하학)
X가 부드러운 사영 복소 대수다양체일 때, X의 모든 호지(Hodge) 류는 대수적이다. 즉, X의 호지 류들은 항상 X의 부분 대수다양체들의 코호몰로지류들의 유리수 위에서의 선형 결합으로 표현될 수 있다.
-> 예시) 어떤 퍼즐이 있는데, 겉으로 보기엔 무작위인 구멍들이 있음.
그 중 특정한 모양(호지 사이클)은 사실 방정식으로 설명할 수 있다는 추측
푸앵카레 정리(위상수학) [증명됨]
3차원 공간의 모든 단일폐곡선이 하나의 점으로 모일 수 있다면 그 공간은 구와 위상적으로 같다.
-> ”우주 끝까지 밧줄을 보내고, 그 밧줄을 다시 회수했을 때 밧줄이 어느 곳에도 걸리지 않는다면 우주는 구 모양이다.“ 라는 추측
양-밀스 질량 간극 가설(입자물리학)
임의의 콤팩트하고 단순한 게이지 군(compact simple gauge group) G에 대해서, 4차원 시공간 속 자명하지 않은 양-밀스 이론이 존재하여, Δ > 0 인 질량 간극을 가짐을 증명하시오. 존재의 증명은 적어도 공리적 양자장론을 구성한 논문들에 인용한 것만큼 강한 공리적 체계를 구성하는 것을 포함해야 한다.
-> 입자 세계의 최소한의 단위에 대한 문제